Efficiently Calculating the Diameter of a Binary Tree in Java: A Step-by-Step Guide

Introduction

In this blog post, we’ll explore how to calculate the diameter of a binary tree using an efficient approach in Java. The diameter of a binary tree is the length of the longest path between any two nodes in the tree. This path may or may not pass through the root.

Understanding the Problem

The diameter of a binary tree can be calculated by finding the maximum value of the following:

1. The diameter of the left subtree.
2. The diameter of the right subtree.
3. The height of the left subtree plus the height of the right subtree plus one (for the current node).

Approach

We’ll use a recursive approach to calculate the diameter and height of the binary tree simultaneously. This approach ensures that we only traverse the tree once, making it efficient with a time complexity of O(n).

Code Explanation

import java.util.LinkedList;
import java.util.Queue;

public class BinaryTreeB {
    static class Node {
        int data;
        Node left;
        Node right;

        Node(int data) {
            this.data = data;
            this.left = null;
            this.right = null;
        }
    }

    static class BinaryTree {         // Diameter of a Binary tree Approach 2 O(n)
        static class InfoD {
            int diam;
            int ht;

            InfoD(int diam, int ht) {
                this.diam = diam;
                this.ht = ht;
            }
        }

        public static InfoD diameterApproach2(Node root) {
            if (root == null) {
                return new InfoD(0, 0);
            }
            InfoD leftInfoD = diameterApproach2(root.left);
            InfoD rightInfoD = diameterApproach2(root.right);

            int diam = Math.max(Math.max(leftInfoD.diam, rightInfoD.diam), leftInfoD.ht + rightInfoD.ht + 1);
            int ht = Math.max(leftInfoD.ht, rightInfoD.ht) + 1;

            return new InfoD(diam, ht);
        }
    }

    public static void main(String args[]) {
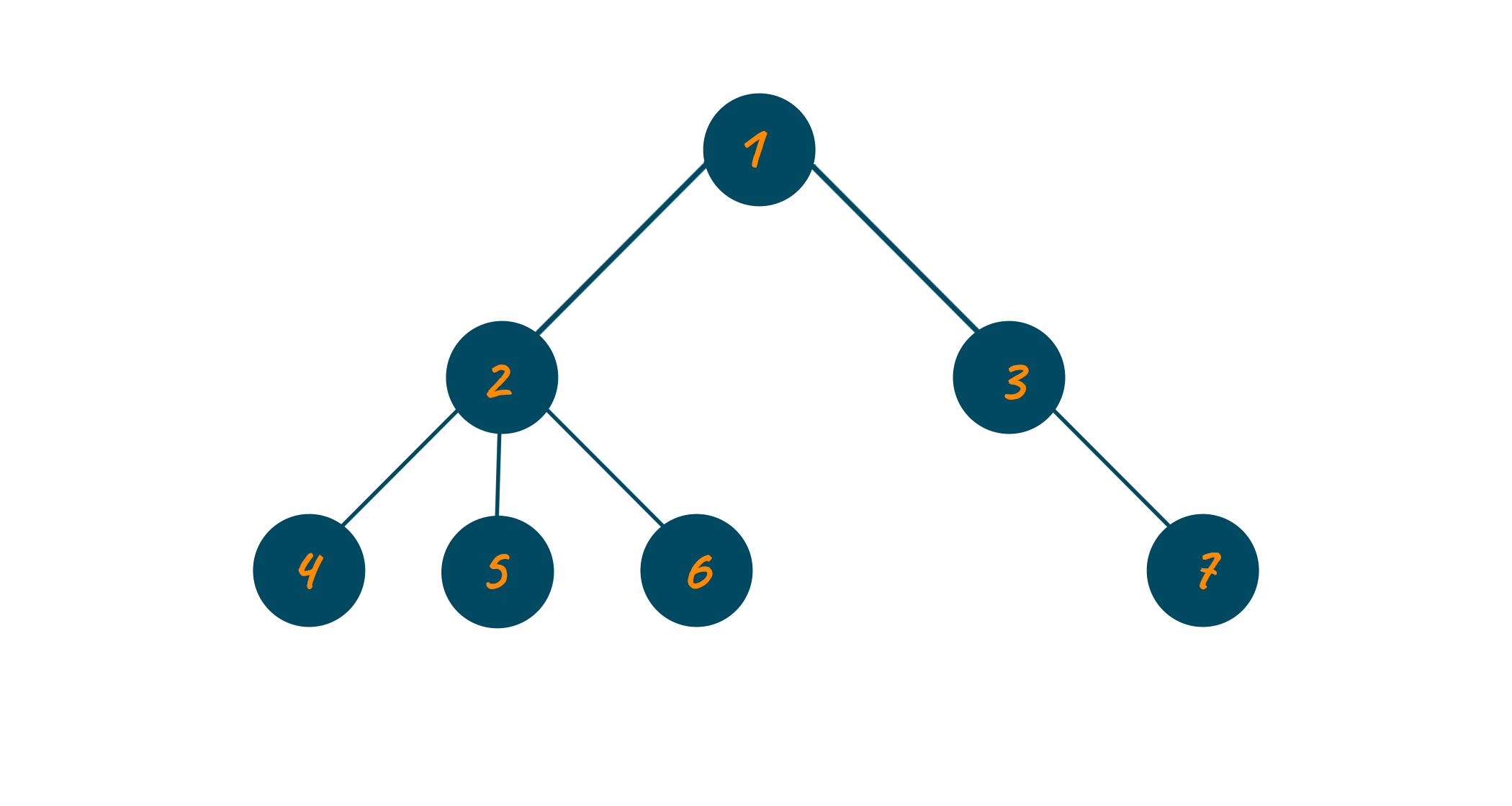
        Node root = new Node(1);

        root.left = new Node(2);
        root.right = new Node(3);

        root.left.left = new Node(4);
        root.left.right = new Node(5);

        root.right.left = new Node(6);
        root.right.right = new Node(7);

        BinaryTree.InfoD result = BinaryTree.diameterApproach2(root);
        System.out.println("Diameter: " + result.diam);
        System.out.println("Height: " + result.ht);
    }
}

Code Breakdown

1. Node Class: This class represents a node in the binary tree. Each node has a data value, a left child, and a right child.

2. BinaryTree Class: This class contains the logic for calculating the diameter and height of the binary tree.

   • InfoD Class: This nested class holds the diameter and height information for a subtree.
   • diameterApproach2 Method: This static method recursively calculates the diameter and height of the binary tree. It returns an InfoD object containing the diameter and height.

3. Main Method: This method creates a sample binary tree and calls the diameterApproach2 method to calculate and print the diameter and height of the tree.

Conclusion

By using this efficient approach, we can calculate the diameter of a binary tree in O(n) time complexity. This method ensures that we only traverse the tree once, making it an optimal solution for this problem.

Feel free to try out the code and modify it to suit your needs. Happy coding!